课程简介
《高等代数(二)》是数学与应用数学、信息与计算科学和统计学等数学类专业的专业基础课之一,是数学类专业报考研究生的必考科目之一,具有高度的抽象性、严密的逻辑性等特点。它一方面为数学专业和其它专业的学习者提供一些进一步学习所需要的基础理论和基本工具,另一方面还对提高学生思维能力,开发学生智能加强“三基”(基础知识、基本理论、基本技能)及培养学生独立工作能力等起着重要的作用.本课程主要讲述内容包括二次型、线性空间、线性变换、λ-矩阵和欧几里得空间,重点围绕线性空间上的可逆变换、合同变换、相似变换、正交变换等线性变换的相关知识,讨论二次型的标准形、矩阵的相似对角化、λ-矩阵的若尔当标准形、有理标准形、实对称矩阵的标准形等核心内容。
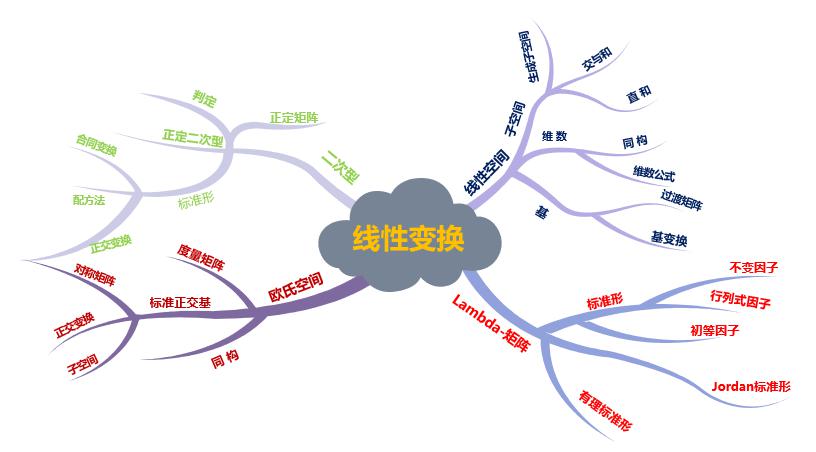
课程大纲

